Đăng vào

Giải phương trình vi phân bằng Matlab ode45

Bài hướng dẫn này sẽ giới thiệu các bạn cách giải phương trình vi phân bậc 2 có hệ số là các hằng số bằng Matlab ode45. Ode là một công cụ được mình sử dụng khá thường xuyên để giải các phương trình vi phân trong matlab.

Chúng ta cần nhớ rằng ode45 chỉ có thể giải được phương trình vi phân bậc nhất. Vì vậy các bạn muốn giải phương trình vi phân bậc thì chúng ta phải chuyển về hệ hai phương trình vi phân bậc nhất.

Phương trình vi phân bậc nhất

Phương trình vi phân bậc nhất có dạng:

dxdt=f(x,t)\frac{dx}{dt}=f\left(x,t\right)

hay viết ở dạng khác:

x˙(t)=f(x,t){\dot{x}}\left(t\right)=f\left(x,t\right)

Ví dụ: để giải phương trình vi phân bậc nhất x˙(t)=3e−t{\dot{x}}\left(t\right)=3e^{-t} với điều kiện ban đầu x(0)=0x\left(0\right)=0 bằng Matlab Ode45

function first_oder_ode
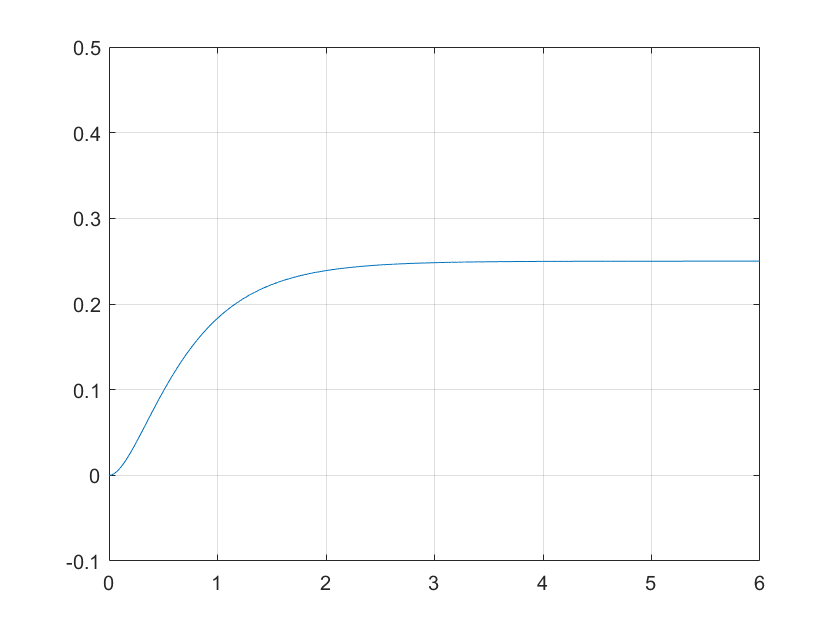
% SOLVE  dx/dt = -3 exp(-t).
% initial conditions: x(0) = 0
t=0:0.001:5;   % time scalex
initial_x=0;
[t,x]=ode45( @rhs, t, initial_x);
plot(t,x);
xlabel('t'); ylabel('x');
grid on
    function dxdt=rhs(t,x)
        dxdt = 3*exp(-t);
    end
end

Kết quả:

ex1

Giải phương trình vi phân bậc hai

Ví dụ: chúng ta tiến hành giải phương trình vi phân bậc hai sau

x¨(t)+5x˙(t)−4x(t)=sin(10t)      (1)\begin{aligned} \ddot{x}\left(t\right)+5\dot{x}\left(t\right)-4x\left(t\right)=sin\left(10t\right) \;\;\;(1) \end{aligned}

Như đã nói ở trên, chúng ta chuyển phương trình vi phân bậc 2 thành hệ hai phương trình vi phân bậc nhất bằng cách đặt ẩn phụ x1,x2x_{1}, x_{2}:

{x1=x(t)x2=x˙(t)⇒{x˙1=x˙(t)x˙2=x¨(t)\begin{aligned} \left\{\begin{matrix} x_{1}=x\left(t\right)\\ x_{2}=\dot{x}\left(t\right) \end{matrix}\right. \Rightarrow \left\{\begin{matrix} \dot{x}_{1}=\dot{x}\left(t\right)\\ \dot{x}_{2}=\ddot{x}\left(t\right) \end{matrix}\right. \end{aligned}

Thế vào phương trình (1) chúng ta có hệ

{x1=x2x2=−5x2+4x1+sin(10t)\begin{aligned} \left\{\begin{matrix} x_{1}=&x_{2}\\ x_{2}=&-5x_{2}+4x_{1}+sin\left(10t\right) \end{matrix}\right. \end{aligned}

Nếu đặt X=[x1x2]X=\begin{bmatrix} x_1\\ x_2 \end{bmatrix} thì hệ trên có thể viết thành dạng phương trình vi phân bậc nhất của biến XX

X=[014−5]X+[0sin(10t)]\begin{aligned} X=\begin{bmatrix} 0 & 1\\ 4 & -5 \end{bmatrix}X+\begin{bmatrix} 0\\ sin\left ( 10t \right ) \end{bmatrix} \end{aligned}

Giải bằng Matlab

function second_oder_ode
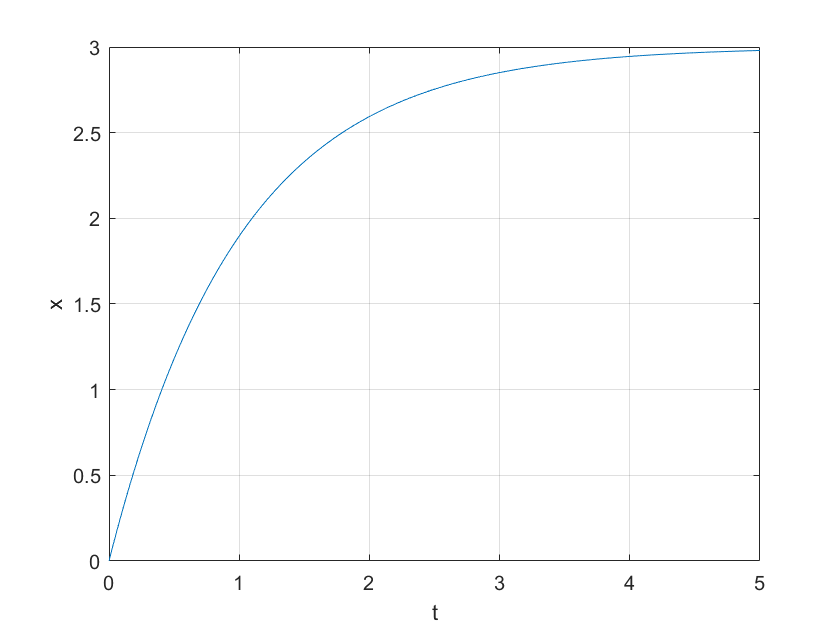
% SOLVE  d2x/dt2+5 dx/dt - 4 x = sin(10 t)
% initial conditions: x(0) = 0, x'(0)=0
t=0:0.001:3;   % time scale
initial_x    = 0;
initial_dxdt = 0;
[t,x]=ode45( @rhs, t, [initial_x initial_dxdt] );
plot(t,x(:,1));
xlabel('t'); ylabel('x');
grid on
    function dxdt=rhs(t,x)
        dxdt_1 = x(2);
        dxdt_2 = -5*x(2) + 4*x(1) + sin(10*t);

        dxdt=[dxdt_1; dxdt_2];
    end
end

Kết quả

ex2

Ứng dụng trong mô phỏng

Dưới đây sẽ là ví dụ dùng ode45 giải phương trình vi phân trong mô phỏng hệ vật nặng, lò xo và giảm chấn

ex3

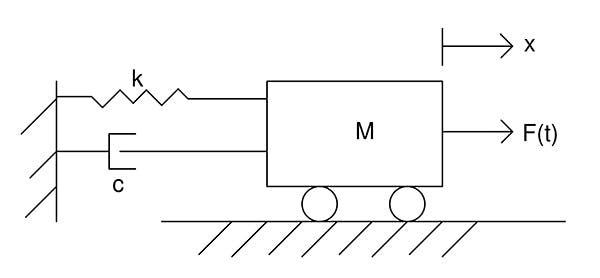
Hệ lò xo giảm chấn có 1 bậc tự do, hệ thống bao gồm xe có khối lượng MM, gắn với lò xo độ cứng kk và giảm chấn có hệ số cc. Khi ngoại lực F(t)F(t) tác động lên xe thì chúng ta cần xác định được vị trí x(t)x(t) của xe. Áp dụng định luật 2 Newton chúng ta xác định được phương trình động lực học của cơ hệ

Mx¨(t)+cx˙(t)+kx(t)=F(t)      (3)\begin{aligned} M\ddot{x}\left(t\right)+c\dot{x}\left(t\right)+kx\left(t\right)=F\left(t\right) \end{aligned} \;\;\; (3)

Viết lại ở dạng hệ phương trình vi phân bậc nhất bằng cách đặt ẩn phụ x1,x2x_{1}, x_{2}:

{x1=x(t)x2=x˙(t)⇒{x˙1=x˙(t)x˙2=x¨(t)\begin{aligned} \left\{\begin{matrix} x_{1}=x\left(t\right)\\ x_{2}=\dot{x}\left(t\right) \end{matrix}\right. \Rightarrow \left\{\begin{matrix} \dot{x}_{1}=\dot{x}\left(t\right)\\ \dot{x}_{2}=\ddot{x}\left(t\right) \end{matrix}\right. \end{aligned}

Thế vào (3) chúng ta được hệ phương trình vi phân bậc nhất

{x˙1=x2x˙2=−cMx2−kMx1+F(t)M\begin{aligned} \left\{\begin{matrix} \dot{x}_1=&x_2\\ \dot{x}_2=&-\dfrac{c}{M}x_2-\dfrac{k}{M}x_1+\dfrac{F\left(t\right)}{M} \end{matrix}\right. \end{aligned}

Hay dạng phương trình trạng thái của cơ hệ

[x˙1x˙2]=[01−kM−cM][x1x2]+[01M]F(t)      (4)\begin{aligned} \begin{bmatrix} \dot{x}_1\\ \dot{x}_2 \end{bmatrix}=\begin{bmatrix} 0 & 1\\ -\dfrac{k}{M} & -\dfrac{c}{M} \end{bmatrix}\begin{bmatrix} x_1\\ x_2 \end{bmatrix}+\begin{bmatrix} 0\\ \dfrac{1}{M} \end{bmatrix}F\left(t\right) \;\;\; (4) \end{aligned}

Code Matlab

function mass_spring_damper()
clear;
close all;

t_start = 0;
t_end   = 6;  %final time in seconds.
time_span =t_start:0.001:t_end;

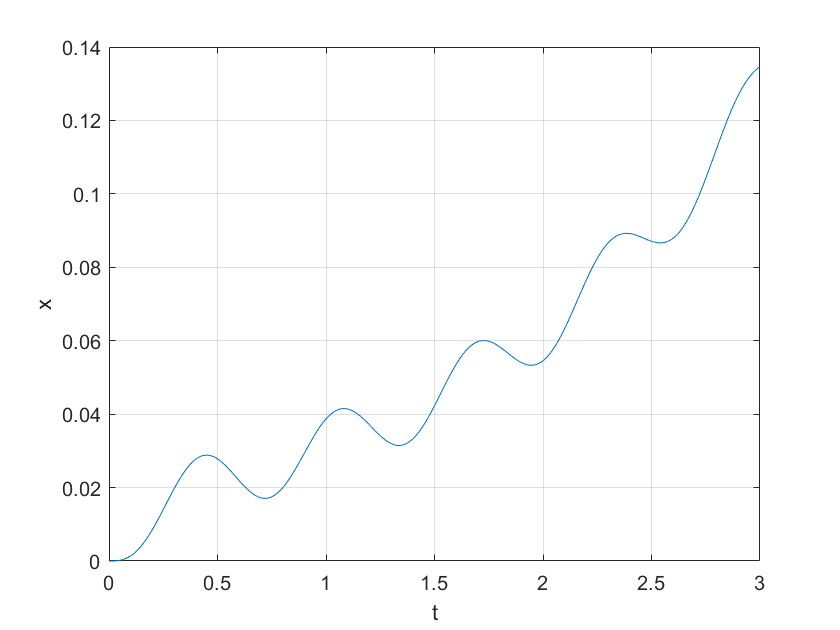
k = 40; % spring stiffness. N/m
m = 5;  % mass, kg
c = 31;

initial_position = 0;
initial_speed    = 0;

x0 = [initial_position  initial_speed];

[t,x]=ode45(@rhs,time_span,x0);
plot(t,x(:,1));
ylim([-.1 .5]);

grid on
%**************************************
% solves m x''+ c x' + k x = f(t)
%**************************************
    function xdot=rhs(t,x)

        xdot_1 = x(2);
        xdot_2 = -(c/m)*x(2) - (k/m)*x(1) + force(t)/m;

        xdot = [xdot_1 ; xdot_2 ];
    end
%********************
% The forcing function, edit to change as needed.
%********************
    function f=force(t)

        P = 100;   % force amplitude
        %f=P*sin(omega*t);

        f=10;  %unit step

        %if t<eps     %impulse
        %   f=1
        %else
        %    f=0;
        %end

        %f=P*t;  %ramp input
    end
end

Kết quả

ex4

CHIA SẺ