- Đăng vào
Lập trình Fuzzy controller không dùng toolbox
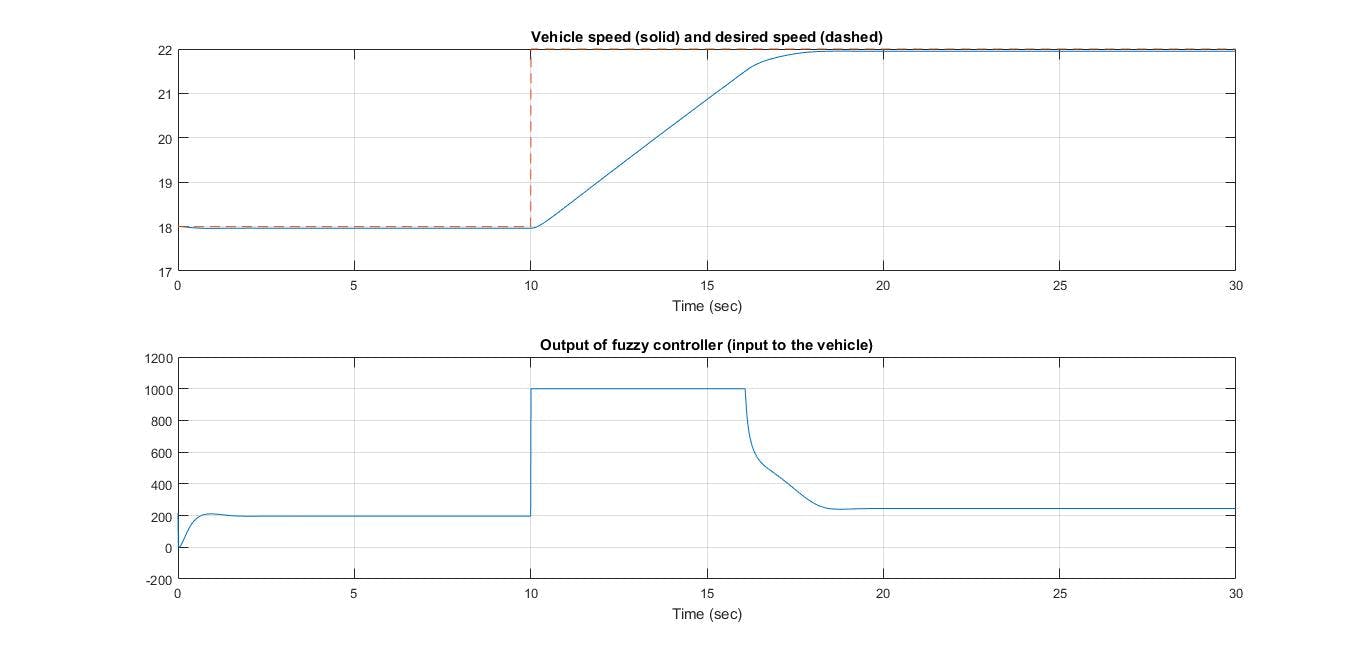
Bài viết này sẽ hướng dẫn thiết kế Fuzzy controller (bộ điều khiển mờ) trên Matlab mà không cần sử dụng toolbox của Matlab. Điều này sẽ giúp các bạn dễ dàng áp dụng lập trình cho vi điều khiển. Ví dụ đơn giản này sẽ điều khiển vận tốc của xe theo một vận tốc mong muốn, kết quả có thể xem hình dưới.
Đề bài
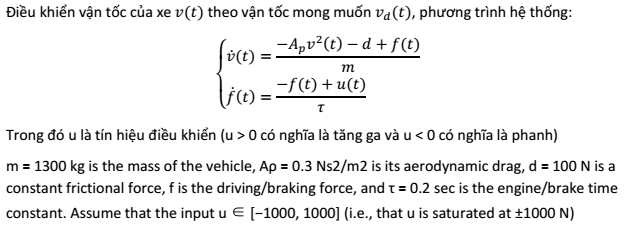
Slides
<iframe
src="//www.slideshare.net/slideshow/embed_code/key/wr7QSvO30ZOf0P"
width="595"
height="485"
frameborder="0"
marginwidth="0"
marginheight="0"
scrolling="no"
style="border:1px solid #CCC; border-width:1px; margin-bottom:5px; max-width: 100%;"
allowfullscreen
></iframe>
Fuzzy controller - Bộ điều khiển mờ from Tien Anh
Code Matlab
%% Fuzzy Cruise Control
% Control Vehical Speed
% Nguyen Van Tien Anh
% 04/03/2016
%%
clear % Clear all variables in memory
clc
% Initialize vehicle parameters
global m Ar tau d
m=1300; % Mass of the vehicle
Ar=0.3; % Aerodynamic drag
tau=0.2; % Engine/brake time constant
d=100; % Constant frictional force
% Initialize parameters for the fuzzy controller
Num_e=5;% Number of Input e
Num_de=5;% Number of Input de
% Gains
g1=1;
g2=0.01;
g0=500;
w_e=1*(1/g1); % Half Width of error (e) triangular
w_de=1*(1/g2);% Half Width of de triangular
w_u=1.6*g0; % Half Width of output triangular
c_e=[-2 -1 0 1 2]*(1/g1);
c_de=[-2 -1 0 1 2]*(1/g2);
rules=[-2 -2 -2 -1 0;
-2 -2 -1 0 1;
-2 -1 0 1 2;
-1 0 1 2 2;
0 1 2 2 2]*g0;
%initialize the simulation:
t=0;
index=1;
tstop=30;
step=0.01; % Integration step size
x=[18;197.2;20]; % Intial condition on state of the car
%% Loop
while t <= tstop
v(index)=x(1); % Output of the car (velocity)
% Desired speed
if t<=10
vd(index)=18;
end
if t>10
vd(index)=22;
end
de_count=0;
e_count=0;
e(index)=vd(index)-v(index);
b(index)=x(3); % Sets the value of the integral of e
% membership function e
if e(index)<=c_e(1)
mfe=[1 0 0 0 0];
e_count=e_count+1;
e_int=1;
elseif e(index)>=c_e(Num_e)
mfe=[0 0 0 0 1];
e_count=e_count+1;
e_int=Num_e;
else
for i=1:Num_e
if e(index)<=c_e(i)
mfe(i)=max([0 1+(e(index)-c_e(i))/w_e]);
if mfe(i)~=0
e_count=e_count+1;
e_int=i;
end
else
mfe(i)=max([0,1+(c_e(i)-e(index))/w_e]);
if mfe(i)~=0
e_count=e_count+1;
e_int=i;
end
end
end
end
% membership function de
if b(index)<=c_de(1)
mfie=[1 0 0 0 0];
de_count=de_count+1;
ie_int=1;
elseif b(index)>=c_de(Num_de)
mfie=[0 0 0 0 1];
de_count=de_count+1;
ie_int=Num_de;
else
for i=1:Num_de
if b(index)<=c_de(i)
mfie(i)=max([0,1+(b(index)-c_de(i))/w_de]);
if mfie(i)~=0
de_count=de_count+1;
ie_int=i;
end
else
mfie(i)=max([0,1+(c_de(i)-b(index))/w_de]);
if mfie(i)~=0
de_count=de_count+1;
ie_int=i;
end
end
end
end
% Calculate control signal
num=0;
den=0;
for k=(e_int-e_count+1):e_int
% Scan over e indices of mfs that are on
for l=(ie_int-de_count+1):ie_int
% Scan over int e indices of mfs that are on
prem=min([mfe(k) mfie(l)]);
% Value of premise membership function
num=num+rules(k,l)*w_u*(prem-(prem)^2/2);
den=den+w_u*(prem-(prem)^2/2);
end
end
u(index)=num/den;
% ODE45
time(index)=t;
F=[(1/m)*(-Ar*x(1)^2 - d + x(2)) ;
(1/tau)*(-x(2)+u(index)) ;
vd(index)-x(1) ];
k1=step*F;
xnew=x+k1/2;
F=[(1/m)*(-Ar*xnew(1)^2 - d + xnew(2)) ;
(1/tau)*(-xnew(2)+u(index)) ;
vd(index)-xnew(1) ];
k2=step*F;
xnew=x+k2/2;
F=[(1/m)*(-Ar*xnew(1)^2 - d + xnew(2)) ;
(1/tau)*(-xnew(2)+u(index)) ;
vd(index)-xnew(1) ];
k3=step*F;
xnew=x+k3;
F=[(1/m)*(-Ar*xnew(1)^2 - d + xnew(2)) ;
(1/tau)*(-xnew(2)+u(index)) ;
vd(index)-xnew(1) ];
k4=step*F;
x=x+(1/6)*(k1+2*k2+2*k3+k4); % Calculated next state
t=t+step; % Increments time
index=index+1; % Increments the indexing term so that
% index=1 corresponds to time t=0.
end
%% Plot graph
subplot(211)
plot(time,v,'-',time,vd,'--')
grid on
xlabel('t(sec)')
title('v(t) (solid) and v_{d}(t)(dashed)');
subplot(212)
plot(time,u,'-k');
grid on
xlabel('t(sec)');
title('Output of fuzzy controller');