- Đăng vào
Áp dụng bộ điều khiển Sliding mode điều khiển động cơ
Lời nói đầu
Việc điều khiển động cơ là một việc rất quan trọng trong điều khiển hệ thống. Nếu chúng ta có thể nắm giữ hoàn toàn động cơ thì việc còn lại là apply vào hệ thống thì sẽ rất là dễ.
Hiện nay, có rất nhiều phương pháp điều khiển có thể áp dụng cho động cơ, phương pháp đơn giản và phổ biến nhất hiện nay chính là sử dụng bộ điều khiển PID. Tuy nhiên trong bài viết này, tôi sẽ hướng dẫn các bạn sử dụng một bộ điều khiển tương đối mạnh và được sử dụng khá phổ biến hiện nay ở các nước phát triển đó là Sliding Mode.
Sliding Mode còn gọi là điều khiển mặt trượt tức là ở đây chúng ta sẽ xây dựng một mặt phẳng sai số và mục tiêu là lái mặt phẳng đó về 0 lúc đó sai số sẽ về 0. Ở đây tôi sẽ không nói quá nhiều vào lý thuyết mà chỉ trình bày cho các bạn một phương pháp đi thông dụng của Sliding Mode và ứng dụng vào điều khiển động cơ.
Nếu bạn nào muốn hiểu hơn về Sliding Mode thì có thể tìm và đọc cuốn sách: Advanced Sliding Mode Control for Mechanical Systems – Design, Analysis and MATLAB Simulation.
Sau đây tôi sẽ trình bày một hướng đi mà theo tôi là được sử dụng tương đối phổ biến trong việc sử dụng Sliding mode cho việc điều khiển động cơ.
- Nhận dạng hệ thống
- Thao tác trên system identification toolbox của matlab
- Tìm tín hiệu điều khiển bằng phương pháp Sliding Mode
- Code mô phỏng
- Code vi điều khiển
- Sự ảnh hưởng của các hệ số
- Kinh nghiệm tune
- Điều khiển vị trí
Nhận dạng hệ thống
Đưa data vào MATLAB
Trước hết để có thể điều khiển được một cái gì đó thì chúng ta cần biết nó là cái gì và hoạt động như thế nào. Tức là chúng ta phải tìm được hàm truyền của hệ thống để biết được mối liên hệ giữa đầu vào và đầu ra.
Có rất nhiều cách để chúng ta xây dựng được hàm truyền hệ thống mà cách làm chính xác và phổ biến nhất đó là việc đi mô hình hóa hệ thống. Tuy nhiên việc mô hình hóa hệ thống không phải là việc mà ai cũng có thể dễ dàng làm được, sẽ tốn của chúng ta rất nhiều thời gian và công sức. Do đó, tôi sẽ hướng dẫn các bạn cách làm thế nào từ một hệ thống có thể đưa ra hàm truyền mà không cần phải mất công đi mô hình hóa nó, đó chính là sử dụng system identification toolbox của Matlab.
Trước hết để nhận dạng được hệ thống thì ta phải biết được nó hoạt động như thế nào bằng cách cấp cho nó một lượng pwm và đo về vận tốc hoạt động của động cơ. Như vậy lúc nhận dạng hệ thống ta sẽ được hàm truyền liên hệ giữa pwm và vận tốc động cơ. Số liệu hoạt động cần được đưa vào workspace của matlab. Ta có thể đưa vào bằng nhiều cách.
Cách 1: lưu số liệu vào một file excel
- Bước 1: chạy và hiển thị thông số lên monitor và sau đó copy vào excel. Trong hình thì data của tôi gồm hai cột, cột đầu tiên là cột pwm và cột thứ hai là cột vận tốc (xung/0.01s)

Bước 2: import data vào trong matlab
Trong matlab tại cửa sổ command window ta sẽ gõ: input=xlsread('D:\Lab\humanoid_robot_leg_sea\data',1,'A1:A2433');
input: tên biếnxlsread: lệnh đọc dữ liệu từ file excel'D:\Lab\humanoid_robot_leg_sea\data': đường dẫn đến file data (file data nằm trong thư mục humanoid_robot_leg_sea- 1: nói cái data là một ma trận 1 cột
A1:A2433: vị trí của data trong file excel
Tương tự ta import thêm biến output: output=xlsread('D:\Lab\humanoid_robot_leg_sea\data',1,'B1:B2433');
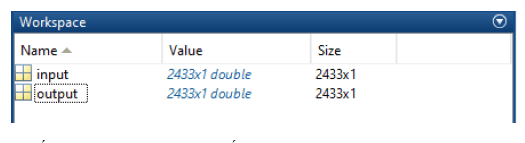
Biến input và output sẽ xuất hiện trong workspace của matlab
Cách 2: Sử dụng GUI để truyền trực tiếp dữ liệu từ vi điều khiển lên Matlab
Cách này là một cách tương đối phức tạp nên mình sẽ không trình bày trong đây. Nếu bạn nào muốn biết rõ thì có thể tìm hiểu về toolbox GUI của Matlab để thực hiện giao tiếp giữa mãy tính và vi điều khiển. Tuy nhiên tôi khuyến khích các bạn sử dụng cách 1 để khỏi mất thời gian và công sức để thiết kế một giao diện tương tác.
Thao tác trên system identification toolbox của matlab
- Bước 1: trong cmd của Matlab ta gõ lệnh: ident để xuất hiện hộp thoại system identification toolbox

- Bước 2: tại ô import data ta chọn Time domain data.

- Bước 3: hộp thoại import data xuất hiện

Tại ô input ta gõ tên biến chứa giá trị pwm vào (biến này phải tồn tại trong workspace nếu không matlab sẽ báo lỗi) (ở đây tôi đã lưu với tên là input)
Tương tự tại ô output sẽ gõ tên biến chứa giá trị vận tốc
Data name: tên của mảng mới chứa giá trị:
inputvàoutput;Starting time: thời điểm ban đầu;Sample time: thời gian lấy mẫu (0.01s). Sau đó nhấn Import rồi close Dữ liệu được import thành công trước khi nhận dạng
Dữ liệu được import thành công trước khi nhận dạng- Bước 4: Tại ô Estimate ta chọn Transfer Function Models

Bước 5: Trong hộp thoại Transfer Function ta tiến hành lựa chọn hàm truyền của hệ thống bằng cách lựa chọn số poles (số nghiệm của mẫu) và số zeros (số nghiệm của tử). Vì hàm truyền giữa vẫn tốc và pwm là hàm bậc một nên tôi sẽ chọn poles là 1 và zeros là 0. Sau đó nhấn Estimate
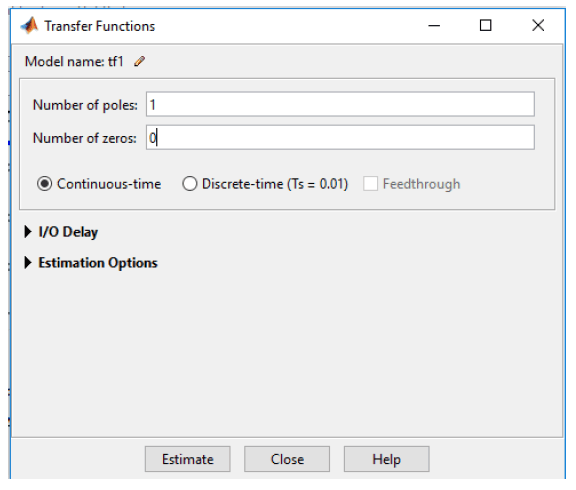
- Bước 6: Chờ quá trình estimate xong thì ta sẽ close tất cả và trở về lại với hộp thoại System Identification. Nhấp đúp chuột vào phần model (tf1) để xem hàm truyền
Model estimate xuất hiện sau khi hệ thống estimate xong
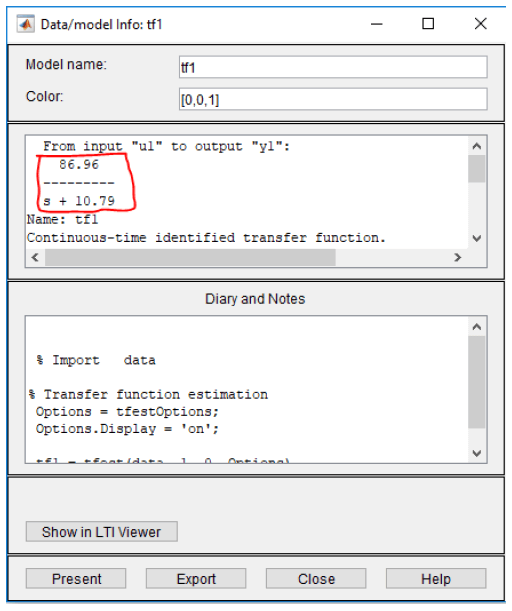
Hàm truyền hệ thống xuất hiện trong hộp thoại Data/model info
Như vậy động cơ của tôi có hàm truyền là:
Tìm tín hiệu điều khiển bằng phương pháp Sliding Mode
Cơ sở lý thuyết
Tiếp theo ta sẽ tiến hành tìm phương trình để tính toán tín hiệu điều khiển PWM cần cho động cơ.
Ta đặt:
Từ phương trình hàm truyền ta có được:
Việc điều khiển sẽ dựa trên sai số của hệ thống. Với sai số là sự chênh lệch giữa giá trị mong muốn () và giá trị đầu ra (). Như vậy ta có:
Vì phương trình hàm truyền chỉ là hàm bậc 1 nên ta đặt mặt phẳng trượt là phương trình bậc 1 theo
Với là mặt trượt và phương trình của nó là do ta tự chọn ( khi hàm truyền là bậc hai thì ta nên chọn ). Mục tiêu là lái mặt phẳng về 0 để dẫn tới sai số bằng 0.
Theo tiêu chuẩn Hurwitz thì hàm sẽ ổn định khi có dạng:
Trong đó hàm:
khi và
khi
Như vậy ta đã tìm được tín hiệu (lượng pwm) cần thiết cho hệ thống, trong đó:
- : là đạo hàm của giá trị mong muốn là giá trị ta đã biết
- : là giá trị feedback về của đầu ra động cơ từ cảm biến
- : là mặt trượt được tính theo công thức
- : là giá trị sai số được tính theo công thức:
- là các hệ số chung ta phải tune để được đáp ứng hệ thống như mong muốn
- : lượng pwm cấp cho động cơ.
Code mô phỏng
%Sliding mode control
%SEA project
%Nguyen Duc Chinh
%19/04/2018
clc;
close all
clear all
%Sampling time
tmax=50;
dt=0.001;
n=round(tmax/dt)+1;
%reference
wr=8;
for i=1:n
r(i)=wr;
end
dr(1)=0; d2r(1)=0; t(1)=0;
for i=2:n
t(i)=t(i-1)+dt;
dr(i)=(r(i)-r(i-1))/dt;
d2r(i)=(dr(i)-dr(i-1))/dt;
end
%controler
c=15; epc=0.5; k=10;
%Initial values
th(1)=0; dth(1)=0;
e(1)=r(1)-th(1); de(1)=dr(1)-dth(1);
%System
s(1)=c*e(1);
u(1)=(dr(1)+(epc*sign(s)+k*s)/c+10.79*th(1))/86.96;
for i=2:n
dth(i)=86.96*u(i-1)-10.79*th(i-1);
th(i)=dth(i)*dt+th(i-1);
e(i)=r(i)-th(i); de(i)=dr(i)-dth(i);
s=c*e(i);
u(i)=(dr(i)+(epc*sign(s)+k*s)/c+10.79*th(i))/86.96;
end
% figure;
% subplot(2,1,1);
plot(t,(th-r));
xlabel('Time (s)');
ylabel('Tracking Error (mm)');
% axis([0,50,-10,10])
% subplot(2,1,2);
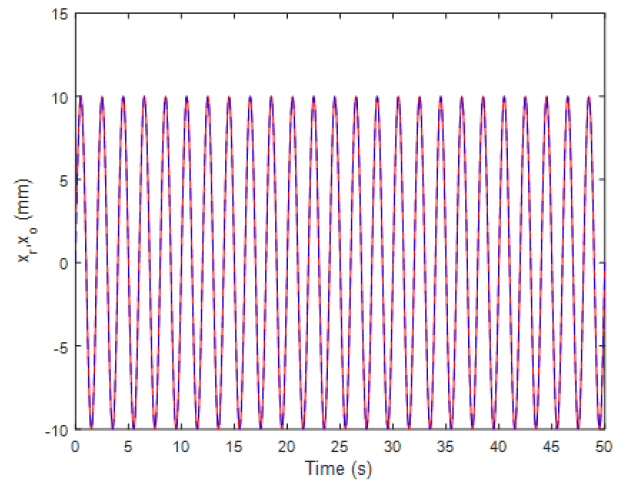
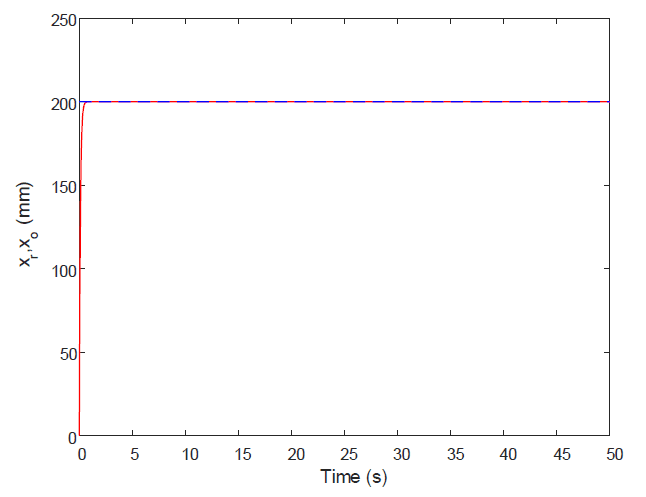
figure;plot(t,th,'r',t,r,'b--');
xlabel('Time (s)');
ylabel('x_r,x_o (mm)');
% axis([0,50,-50,50])
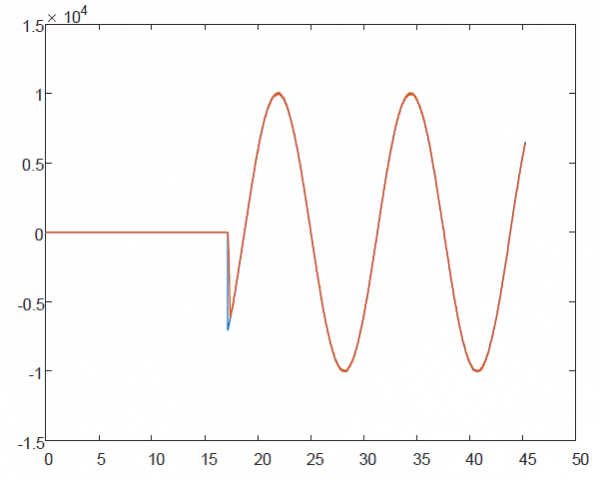
figure;plot(t,u);
xlabel('Time (s)');
ylabel('T_M(N.mm)');
% axis([0,30,-30,30])
figure;plot(e,de);
xlabel('e');
ylabel('de');
% axis([-0.4,0.6,-1.8,0.2])
Code vi điều khiển
dvelo = 89.99 * output - 16.26 * velo;
velo = encoder_1 - pre_encoder_1;
pre_encoder_1 = encoder_1;
er = velo_setpoint - velo;
s = c_velo * er ;
if (s > 0) {
output = ((epc_velo + k_velo * s) / c_velo + 10.79 * velo) / 86.96;
}
else {
output = ((-epc_velo + k_velo * s) / c_velo + 10.79 * velo) / 86.96;
}
Với các hệ số:
c_velo= 15;epc_velo= 0.1;k_velo= 150;
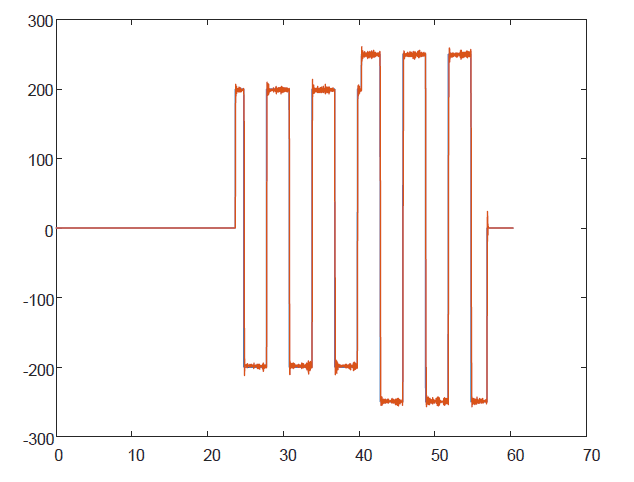
Sự ảnh hưởng của các hệ số
- ảnh hưởng đến khả năng đáp ứng giống như khâu P trong PID
- ảnh hưởng đến khả năng giảm Steady state error giống khâu I trong PID
- ảnh hưởng đến khả năng bù giống khâu D trong PID, e càng lớn thì đáp ứng càng nhanh nhưng sẽ gây ra dao động lớn và ngược lại.
Kinh nghiệm tune
Tăng dần lên để hệ đáp ứng được giá trị mong muốn, lúc đó sẽ gây ra steady state error. Khi đó ta tăng c dần lên để giảm steady state error (bình thường mình chỉ cần tune hai thành phần này là đủ), khâu e nên lấy nhỏ để không gây ra chattering.
Điều khiển vị trí
Để điều khiển vị trí thì ta làm tương tự như vận tốc để tìm công thức để tính (PWM) cần thiết. Tuy nhiên vì hàm truyền vị trí là hàm bậc 2 nên nên được tính bằng công thức:
Làm tương tự các bạn sẽ tính được tín hiệu u theo công thức: