Đăng vào

Dùng Matlab giải quyết bài toán tối ưu trong kỹ thuật

Giới thiệu

Khi quyết định lựa chọn một phương án thì chúng ta luôn cân nhắc giữa hai yếu tố: lợi ích đạt được và chi phí phải bỏ ra. Phương án tối ưu là giải pháp mà cực tiểu chi phí và cực đại về lợi ích đem lại. Trong các bài toán kỹ thuật việc lựa chọn phương án tối ưu sẽ đưa đến một sản phẩm tốt theo yêu cầu đặt ra.

Matlab Optimate

Maltab là một phần mềm được sử dụng khá phổ biến trong kỹ thuật, phần mềm này cũng hỗ trợ tính toán tối ưu với Optimization Toolbox. Để xây dựng một bài toán tối ưu bạn cần tìm ra 3 yếu tố:

  • Hàm tối ưu: Thông thường là cực đại hoặc cực tiểu hàm tối ưu.
  • Biến tối ưu: Các thông số cần xác định để đạt được hàm tối ưu.
  • Các điều kiện ràng buộc: các mối quan hệ giữa các biến tối ưu.

Ví dụ một bài toán tối ưu

Để minh họa mình sẽ đưa ra một bài toán tối ưu một kết cấu mà mình đã thực hiện.

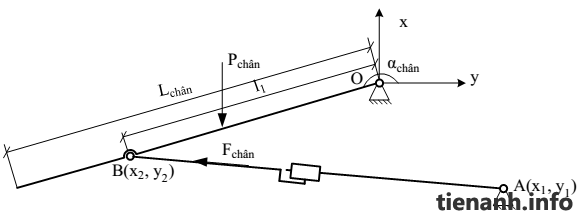
co cau nang ha chan

Bài toán tối ưu đặt ra là:

Tìm vị trí 2 điểm A và B để khi cơ cấu hoạt động: alphachan=150odiv260oalpha_{chan}=150^{o}div260^{o} thì giá trị lực tác dụng FchanF_{chan} để cân bằng với tải Pchan P_{chan} là nhỏ nhất. Tính toán ta được hàm tối ưu và các điều kiện ràng buộc:

Sau khi tìm được các yếu tố ta tiến hành viết chương trình tìm giá trị tối ưu trong Matlab

Chương trình tối ưu trong Matlab

Upload code trước...

chan_Optimate.m

chan_Optimate.m
clear all
clc
global chan_Lfix chan_P chan_L chan_angle_min chan_angle_max chan_H alpha;
chan_Lfix = 215; % chieu dai co dinh Linear actuator
chan_P = 31.3/2; % Trong luong 1 chan
chan_L = 455; % Chieu dai khau nang do chan
chan_H = 0; % Do chenh lech chieu cao giua 2 khop
chan_angle_min = 150; % Goc nghieng min
chan_angle_max = 260; % Goc nghieng max
angle_zero = 180;
% Cac rang buoc tuyen tinh
x0 = [10,-150,300];     % Make a starting guess at the solution
lb = [10,-150,300];
ub = [90,-50,440];

options = optimoptions(@fmincon,'Algorithm','sqp');
[x,fval] = ...
fmincon(@chan_objfun,x0,[],[],[],[],lb,ub,@chan_confun,options);
% Lam tron so lieu
x = round(x);
Fmax = chan_objfun(x);
% Tinh toan hanh trinh actuator
Lmin = sqrt((x(1) - x(3)*cosd(chan_angle_max))^2 ...
             +(x(2) - x(3)*sind(chan_angle_max))^2);
Lmax = sqrt((x(1) - x(3)*cosd(chan_angle_min))^2 ...
             +(x(2) - x(3)*sind(chan_angle_min))^2);
L0 = sqrt((x(1) - x(3)*cosd(angle_zero))^2 ...
             +(x(2) - x(3)*sind(angle_zero))^2);
% Hien thi ket qua tinh toan
display(['gia tri x1 y1 l1: ' num2str(x)]);
display(['Fmax: ' num2str(Fmax)]);
display(['Lmin: ' num2str(Lmin)]);
display(['Lmax: ' num2str(Lmax)]);
display(['L0: ' num2str(L0)]);
display(alpha);

% Ve do thi Luc
angle = 150:0.5:260;
x1 = x(1);
y1 = x(2);
l1 = x(3);
Mtai = chan_P*chan_L/2;
f = Mtai*(cosd(angle)).*sqrt((y1-l1*sind(angle)).^2 + (x1 - l1*cosd(angle)) ...
    .^2)/l1./(y1*cosd(angle) - x1*sind(angle));
figure(1)
hold on
grid on;
xlim([-50;100]);
plot(angle-180,f,'k','LineWidth',2);
xlabel('alpha_c_h_a_n');
ylabel('F_c_h_a_n');
title('Nang ha chan');

chan_objfun.m

chan_objfun.m
function f = chan_objfun(x)
% x(1) = x1
% x(2) = y1
% x(3) = l1
global chan_P chan_L alpha
Mtai = chan_P*chan_L/2;
alpha = 150;
% Ham toi uu
f = abs(cosd(alpha))*Mtai*sqrt((x(2)-x(3)*sind(alpha))^2 + (x(1) - x(3)*cosd(alpha)) ...
    ^2)/x(3)/abs(x(2)*cosd(alpha) - x(1)*sind(alpha));

chan_confun.m

chan_confun.m
function [c, ceq] = chan_confun(x)
% Nonlinear inequality constraints
% x(1) = x1
% x(2) = y1
% x(3) = l1
global chan_Lfix chan_angle_min chan_angle_max;
Lmin = sqrt((x(1) - x(3)*cosd(chan_angle_max))^2 ...
        +(x(2) - x(3)*sind(chan_angle_max))^2);
Lmax = sqrt((x(1) - x(3)*cosd(chan_angle_min))^2 ...
             +(x(2) - x(3)*sind(chan_angle_min))^2);

c = [Lmax + chan_Lfix - 2*Lmin; x(2)+x(1)*tand(30)];
% Nonlinear equality constraints
ceq = [];

CHIA SẺ