Đăng vào

Robot hai chân - Phân tích động học thuận

Bài viết này giới thiệu các bạn phân tích động học thuận của robot hai chân với tổng cộng 12 bậc tự do và mô phỏng trong Matlab. Thông số động học của robot là của robot UXA-90, đây là một phần nhỏ trong dự án mà mình đang thực hiện.

Phân tích động học thuận

Thông số động học cơ bản của robot được trình bày trong Hình 1

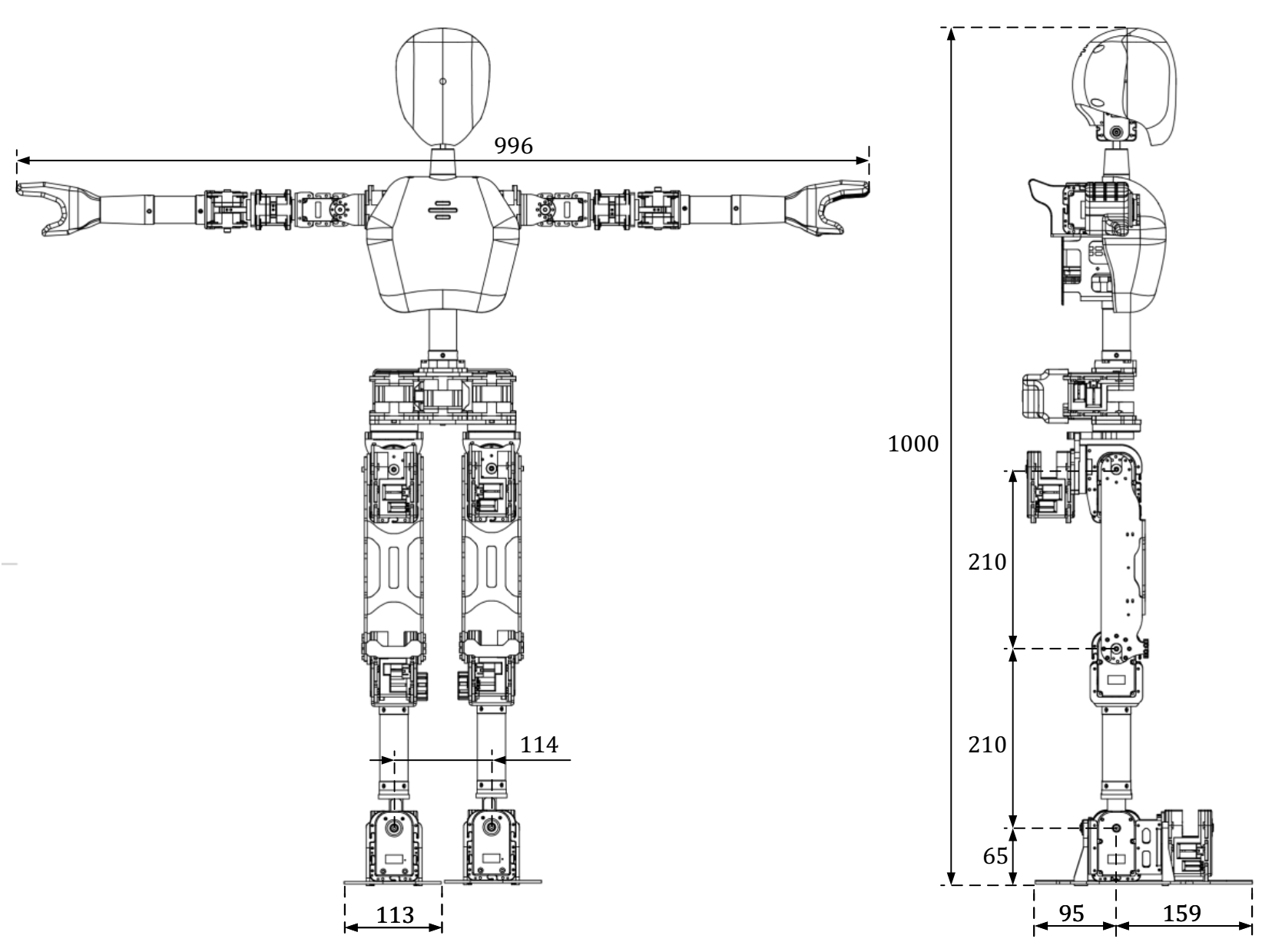
UXA-Kinematic

Hình 1

Trong phạm vi bài viết này chỉ giải quyết động học cho hai chân, phần thân trên mình xem như cố định, tọa độ đặt lên hai chân được thể hiện trong Hình 2. Tọa độ đặt lên mỗi khớp được đặt theo quy ước Denavit-Hartenberg với các thông số trong Bảng 1. Hệ tọa độ toàn cục (world coordination) là O0O_0 Hệ tọa độ robot đặt tại giữa hông O1O_1

UXA Coordinateion

Bảng 1. Thông số DH của robot hai chân

Trong đó: l1=0.057ml_1 = 0.057 m, l2=0.042ml_2 = 0.042 m, l3=l4=0.21ml_3 = l_4 = 0.21 m, l5=0.065ml_5 = 0.065 m

Theo quy ước DH-Modified, ma trận chuyển đổi từ tọa độ i−1i-1 sang tọa độ ii

i−1Ti=[cos⁡θi−sin⁡θi0aicos⁡αisin⁡θicos⁡αicos⁡θi−sin⁡αi−disin⁡αisin⁡αisin⁡θisin⁡αicos⁡θicos⁡αidicos⁡αi0001]      (1)\begin{aligned} ^{i-1}T_{i}=\begin{bmatrix}\cos{\theta_i} & -\sin{\theta_i} & 0 & a_i \\ \cos{\alpha_i}\sin{\theta_i} & \cos{\alpha_i}\cos{\theta_i} & -\sin{\alpha_i} & -d_i\sin{\alpha_i} \\ \sin{\alpha_i}\sin{\theta_i} & \sin{\alpha_i}\cos{\theta_i} & \cos{\alpha_i} & d_i\cos{\alpha_i}\\ 0 & 0 & 0 & 1 \end{bmatrix} \;\;\;(1) \end{aligned}

Phương trình động học thuận của chân trái là (2) và chân phải là (3)

FK(q)=0T1∏i=27i−1Ti=[nsap0001]      (2)\begin{aligned} FK(q)=^{0}T_1{\prod_{i=2}^7}{^{i-1}T_i}=\begin{bmatrix}n & s & a & p \\0 & 0 & 0 &1 \end{bmatrix} \;\;\;(2) \end{aligned} FK(q)=0T1∏i=813i−1Ti=[nsap0001]      (3)\begin{aligned} FK(q)=^{0}T_1{\prod_{i=8}^{13}}{^{i-1}T_i}=\begin{bmatrix}n & s & a & p \\0 & 0 & 0 &1 \end{bmatrix} \;\;\;(3) \end{aligned}

Lập trình bằng Matlab

Để lập trình mô phỏng trong Matlab, chúng ta tạo đối tượng uLINK trong là một mảng kiểu struct gồm các thuộc tính :

  • namename : tên của khớp
  • mm : khối lượng của link
  • sistersister và childchild là id của link liên quan với link hiện tại, mục đích là để thực hiện các giải thuật đệ quy trong tính toán động học của robot
  • TT : ma trận biến đổi của khâu
  • rotrot : ma trận xoay được thiết đặt cho việc vẽ mô hình, không liên quan đến bài toán động học
  • ubub (upper boundary) và lblb (lower boundary) là giới hạn góc quay của khớp

Khởi tạo một đối tượng uLINK trong Matlab

uLINK = struct('name','BODY','m',3.5,'sister',0,'child',2,'q',0,'DH',[0, 0, 0, 0],'T',eye(4),'rot',rotz(90),'ub',pi/2,'lb',-pi/2);

Hình 3

Hình 3 thể hiện cấu tên và ID các link của robot

Đoạn code dưới dây thể hiện tác dụng của việc sister và child của từng link trong chương trình mô phỏng. Cấu trúc này cho phép việc lập trình trở nên ngắn gọn hơn.

function FindMother(j)
global uLINK
% recursive structure
if j ~= 0
    if j == 1
        uLINK(j).mother = 0;
    end
    if uLINK(j).child ~= 0
        uLINK(uLINK(j).child).mother = j;
        FindMother(uLINK(j).child);
    end
    if uLINK(j).sister ~= 0
        uLINK(uLINK(j).sister).mother = uLINK(j).mother;
        FindMother(uLINK(j).sister);
    end
end

Hình 4

Code mô phỏng động học thuận các bạn download ở cuối bài viết. Download xong thì chay file UXA_FK_demo.m. Kết quả mô phỏng

Hình 5. Kết quả mô phỏng động học

CHIA SẺ