Đăng vào

Điều khiển LQR mô hình con lắc ngược

Bài viết này sẽ hướng dẫn các bạn điều khiển mô hình con lắc gắn trên xe bằng bộ điều khiển LQR trên Matlab. Đầu tiên mình sẽ phân tích để tìm ra phương trình trạng thái của hệ thống sau đó viêt code mô phỏng trong matlab.

Mô hình hệ thống

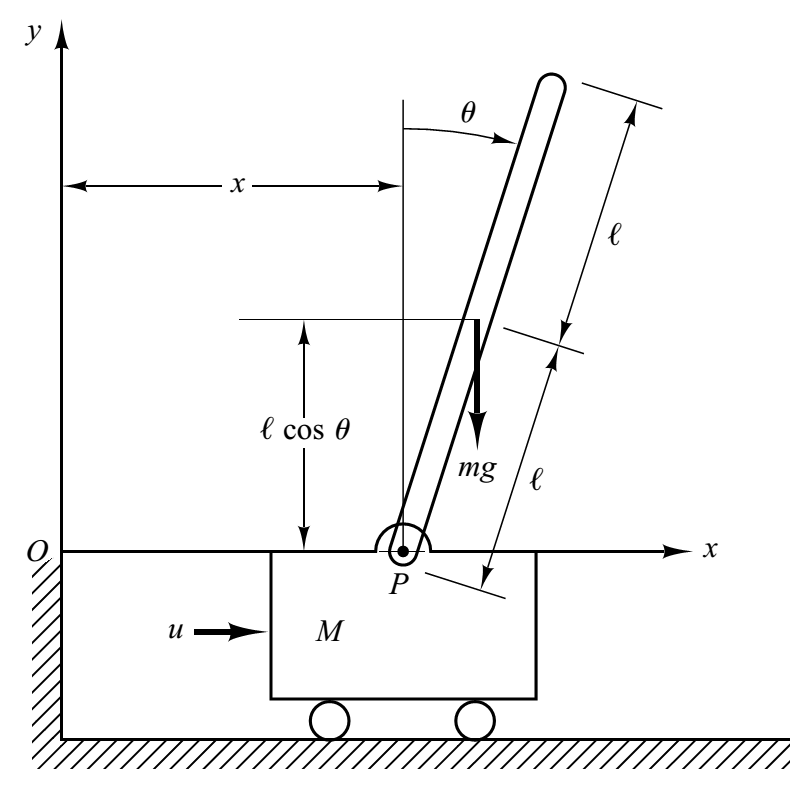
invert-pendulum

Trong đó:

  • uu là lực tác dụng lên xe
  • xx là vị trí của xe
  • θ\theta là góc nghiêng của con lắc
  • mm là khối lượng của con lắc
  • MM là khối lượng của xe
  • II là moment quán tính của con lắc.
  • L=2lL=2l là chiều dài của con lắc ngược

Phương trình động lực học

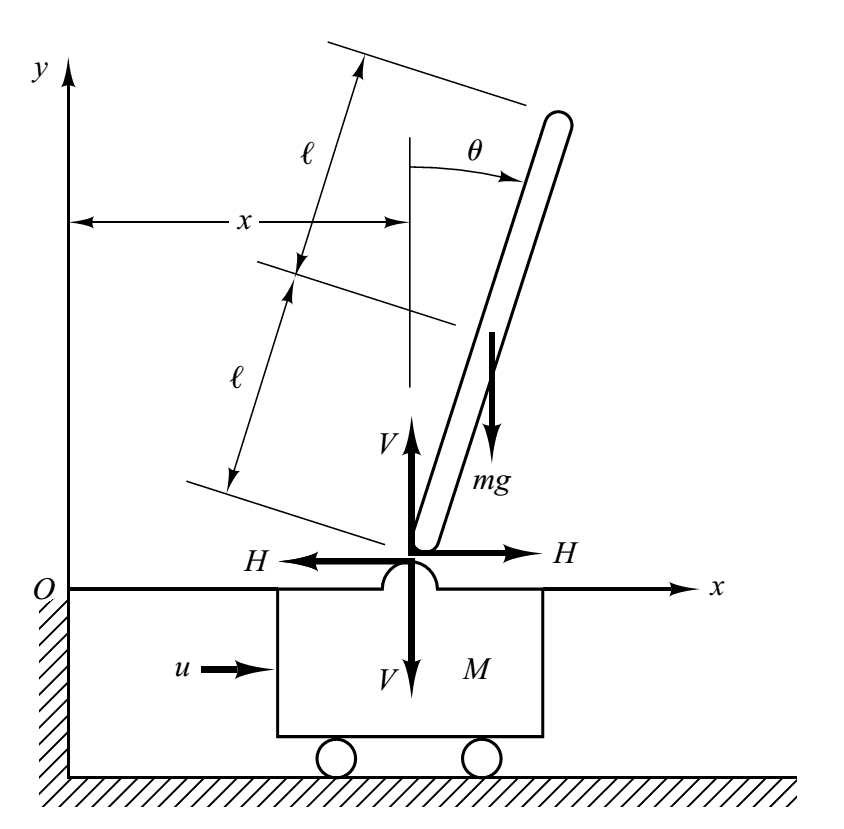
invert-pendulum-2

Phương pháp 1

Áp dụng các định luật Newton

Phân tích lực tác động lên từng thành phần của hệ thống là xe và con lắc. Tại khớp nối sẽ xuất hiện các cặp phản lực tương ứng triệt tiêu nhau là HH và VV.

Giả sử con lắc có dạng thanh thẳng đồng chất, trọng tậm GG nằm ở chính giữa thanh với tọa độ:(xG,yG)\left(x_{G},y_{G}\right):

{xG=x+lsinθyG=lcosθ      (1)\begin{aligned} \begin{cases}x_{G}=x+lsin\theta\\y_{G}=lcos\theta\end{cases}\qquad \;\;\;(1) \end{aligned}

Con lắc chuyển động xoay quanh trọng tâm GG và chuyển động theo xe: Chuyển động xoay:

Iθ¨=Vlsin⁡θ−Hlcos⁡θ      (2)\begin{aligned} I\ddot{\theta}=Vl\sin\theta-Hl\cos\theta\qquad \end{aligned} \;\;\;(2)

Chuyển động theo phương ngang:

x¨G=d2(xG)dt2=H      (3)⇔d2(x+lsin⁡θ)dt2=H\begin{aligned} \ddot{x}_{G}=\frac{d^{2}\left(x_{G}\right)}{dt^{2}}&=H\qquad \;\;\;(3)\\ \Leftrightarrow \frac{d^{2}\left(x+l\sin\theta\right)}{dt^{2}}&=H \end{aligned}

Chuyển động theo phương đứng:

y¨G=d2(yG)dt2=HV−mg      (4)⇔d2(lcos⁡θ)dt2=V−mg\begin{aligned} \ddot{y}_{G}=\frac{d^{2}\left(y_{G}\right)}{dt^{2}}&=HV-mg\qquad \;\;\;(4)\\ \Leftrightarrow\frac{d^{2}\left(l\cos\theta\right)}{dt^{2}}&=V-mg \end{aligned}

Phương trình chuyển động của xe:

Mx¨=u−H      (5)\begin{aligned} M\ddot{x}=u-H\qquad\end{aligned} \;\;\;(5)

Mục tiêu điều khiển là duy trì con lắc nằm ở phương thẳng đứng, chúng ta giả sử rằng θ(t)\theta\left(t\right) và θ˙(t)\dot{\theta}\left(t\right) nhỏ nên có thể xem sin⁡θ≈θ,cos⁡θ≈1,θθ˙≈0\sin\theta\approx\theta,\cos\theta\approx1,\theta\dot{\theta}\approx0.

Phương trình động lực học của hệ thống:

(2)⇔Iθ¨=Vlθ−Hl      (6)(3)⇔m(x¨+lθ¨)=H      (7)(4)⇔0=V−mg      (8)\begin{aligned} \left(2\right)&\Leftrightarrow I\ddot{\theta}=Vl\theta-Hl\qquad \;\;\;(6) \\ \left(3\right)&\Leftrightarrow m\left(\ddot{x}+l\ddot{\theta}\right)=H\qquad \;\;\;(7)\\ \left(4\right)&\Leftrightarrow 0=V-mg\qquad \;\;\;(8) \end{aligned}

Kết hợp (5) và (7) ta được:

(M+m)x¨+mlθ¨=u      (9)\begin{aligned} \left(M+m\right)\ddot{x}+ml\ddot{\theta}=u\qquad \;\;\;(9) \end{aligned}

Kết hợp (6), (7) và (8) :

(I+ml2)θ¨+mlx¨=mglθ      (10)\begin{aligned} \left(I+ml^{2}\right)\ddot{\theta}+ml\ddot{x}=mgl\theta\qquad \;\;\; (10) \end{aligned}

Phương pháp 2

Áp dụng phương trình Euler-Lagrange (đang cập nhật)

Laplace 2 vế của (9) và (10):

[θ˙θ¨x˙x¨]=[0100(M+m)mglI(M+m)+Mml20000001−m2gl2I(M+m)+Mml2000][θθ˙xx˙]+[0−mlI(M+m)+Mml20I+ml2I(M+m)+Mml2]u\begin{aligned} \begin{bmatrix}\dot{\theta} \\ \ddot{\theta} \\\dot{x} \\ \ddot{x} \end{bmatrix}=\begin{bmatrix}0&1&0&0 \\ \frac{\left(M+m\right)mgl}{I\left(M+m\right)+Mml^{2}}&0&0&0 \\0&0&0&1\\ -\frac{m^{2}gl^{2}}{I\left(M+m\right)+Mml^{2}}&0&0&0 \end{bmatrix}\begin{bmatrix} \theta \\ \dot{\theta} \\x \\ \dot{x} \end{bmatrix}+\begin{bmatrix}0 \\ -\frac{ml}{I\left(M+m\right)+Mml^{2}} \\0 \\ \frac{I+ml^{2}}{I\left(M+m\right)+Mml^{2}} \end{bmatrix}u\qquad \end{aligned}

Bộ điều khiển LQR

Đang cập nhật

Code Matlab

Inverted_Pendulum.m

%Single Link Inverted Pendulum Control
clc;
clear all;
global A B C D;
%Single Link Inverted Pendulum Parameters
g=9.8;
M=1.0;
m=0.1;
L=0.5;
% Fc=0.0005;
% Fp=0.000002;
I=1/12*m*L^2;
l=1/2*L;
t1=m*(M+m)*g*l/[(M+m)*I+M*m*l^2];
t2=-m^2*g*l^2/[(m+M)*I+M*m*l^2];
t3=-m*l/[(M+m)*I+M*m*l^2];
t4=(I+m*l^2)/[(m+M)*I+M*m*l^2];
A=[0,1,0,0;
   t1,0,0,0;
   0,0,0,1;
   t2,0,0,0];
B=[0;t3;0;t4];
C=[1,0,0,0;
   0,0,1,0];
D=[0;0];

% Declare the LQR controller
Q=[1,0,0,0;   %100,10,1,1 express importance of theta,dtheta,x,dx
   0,1,0,0;
   0,0,1,0;
   0,0,0,1];
R=[5];
% Calculate gain of LQR
K=lqr(A,B,Q,R);
e1_1=0;
e2_1=0;
e3_1=0;
e4_1=0;
u_1=0;
% xk=[-10/57.3,0,0.20,0];   %Initial values
%xk=[-0.4,0,0.20,0];
xk=[0,0.5,0,0];
ts=0.01;
for k=1:3000
    time(k)=k*ts;
    Tspan=[0 ts];
    control_input=u_1;
    [t,x]=ode45('pendulum',Tspan,xk,[],control_input);
    length(xk)
    xk=x(length(x),:);

    r1(k)=0;    %Pendulum Angle
    r2(k)=0;    %Pendulum Angle Rate
    r3(k)=1;    %Car Position
    r4(k)=1;    %Car Position Rate

    x1(k)=xk(1);
    x2(k)=xk(2);
    x3(k)=xk(3);
    x4(k)=xk(4);

    e1(k)=r1(k)-x1(k);
    e2(k)=r2(k)-x2(k);
    e3(k)=r3(k)-x3(k);
    e4(k)=r4(k)-x4(k);
% Design different controllers
 u(k)=K(1)*e1(k)+K(2)*e2(k)+K(3)*e3(k)+K(4)*e4(k);
    if u(k)>=10
        u(k)=10;
    elseif u(k)<=-10
        u(k)=-10;
    end
	e1_1=e1(k);
	e2_1=e2(k);
	e3_1=e3(k);
	e4_1=e4(k);
	u_1=u(k);
end
figure(1);
subplot(411);
plot(time,r1,'k',time,x1,'k');      %Pendulum Angle
xlabel('time(s)');ylabel('Angle');
subplot(412);
plot(time,r2,'k',time,x2,'k');      %Pendulum Angle Rate
xlabel('time(s)');ylabel('Angle rate');
subplot(413);
plot(time,r3,'k',time,x3,'k');      %Car Position
xlabel('time(s)');ylabel('Cart position');
subplot(414);
plot(time,r4,'k',time,x4,'k');      %Car Position Rate
xlabel('time(s)');ylabel('Cart rate');
figure(2);
plot(time,u,'k');                   %Force F change
xlabel('time(s)');ylabel('Force');
grid on;

pendulum.m

function dx=pendulum(t,x,flag,control_input)
global A B C D;
u=control_input;
dx=zeros(4,1);
%State equation for one link inverted pendulum
dx=A*x+B*u;
end

CHIA SẺ