- Đăng vào
Điều khiển PID mô hình con lắc ngược
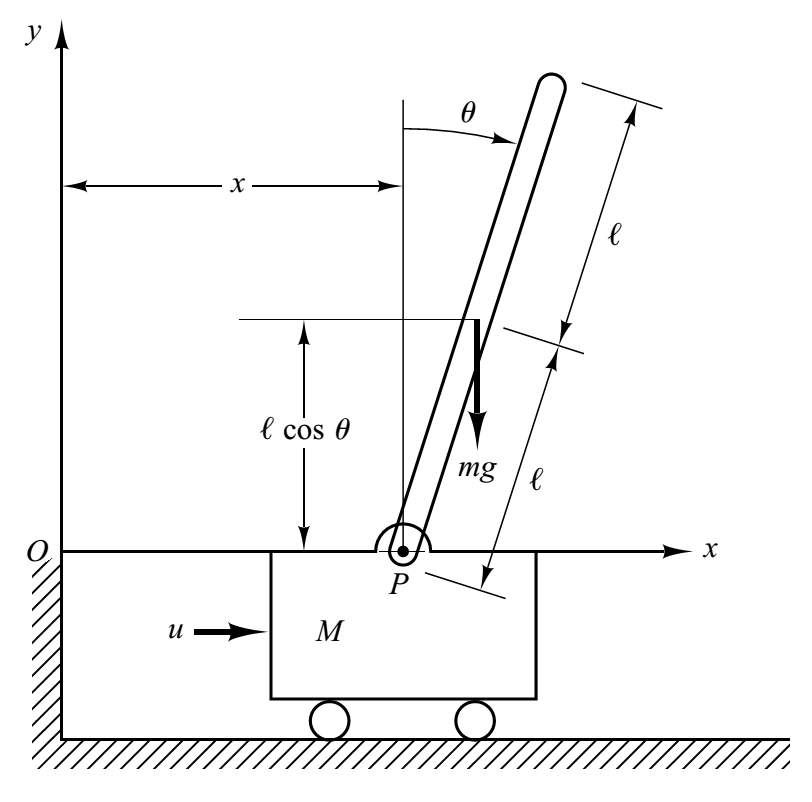
Ở bài viết này sẽ hướng dẫn các bạn viết chương trình mô phỏng con lắc ngược trong Matlab. Mô hình sử dụng bộ điều khiển PID. Phần tính toán động lực học các bạn xem ở bài viết Điều khiển LQR mô hình con lắc ngược
Code Matlab
Inverted_Pendulum.m
%Single Link Inverted Pendulum Control
clc;
clear all;
close all
global A B C D;
%Single Link Inverted Pendulum Parameters
g=9.8;
M=0.5;
m=0.2;
L=0.3;
% Fc=0.0005;
% Fp=0.000002;
I=1/12*m*L^2;
l=1/2*L;
t1=m*(M+m)*g*l/[(M+m)*I+M*m*l^2];
t2=-m^2*g*l^2/[(m+M)*I+M*m*l^2];
t3=-m*l/[(M+m)*I+M*m*l^2];
t4=(I+m*l^2)/[(m+M)*I+M*m*l^2];
A=[0,1,0,0;
t1,0,0,0;
0,0,0,1;
t2,0,0,0];
B=[0;t3;0;t4];
C=[1,0,0,0;
0,0,1,0];
D=[0;0];
Kp = [10 1];
Kd = [1 1];
Ki = [1 1];
desired = [0 1];% theta theta_dot x x_dot
init=[0.2,0.1,0,0];
dt=0.01;
N = 2000;
% pre-assign all the arrays to optimize simulation time
Prop = zeros(N+1,2);
Der = zeros(N+1,2);
Int = zeros(N+1,2);
I = zeros(N+1,2);
PID = zeros(N+1,1);
FeedBack = zeros(N+1,2);
Output = zeros(N+1,4);
Error = zeros(N+1,2);
time = zeros(N+1,1);
Output(1,:) = init;
for k=1:N
time(k+1)=k*dt;
Tspan=[0 dt];
control_input=PID(k);
[t,x]=ode45('pendulum',Tspan,Output(k,:),[],control_input);
FeedBack(k+1,:)=x(end,[1,3]);
Output(k+1,:) = x(end,:);
Error(k+1,:) = desired - FeedBack(k+1,:); % error entering the PID controller
Prop(k+1,:) = Error(k+1,:);% error of proportional term
Der(k+1,:) = (Error(k+1,:) - Error(k,:))/dt; % derivative of the error
Int(k+1,:) = (Error(k+1,:) + Error(k,:))*dt/2; % integration of the error
I(k+1,:) = sum(Int); % the sum of the integration of the error
PID(k+1) = -Kp*Prop(k+1,:)' - Ki*I(k+1,:)'- Kd*Der(k+1,:)'; % the three PID terms
% Limit control signal
if PID(k+1)>=10
PID(k+1)=10;
elseif PID(k+1)<=-10
PID(k+1)=-10;
end
end
% Reference = desired.*ones(N+1,4);
Reference = zeros(N+1,2);
Reference(:,1) = desired(1)*ones(N+1,1);
Reference(:,2) = desired(2)*ones(N+1,1);
figure(1)
subplot(4,1,1)
hold on
plot(time,Reference(:,1),'--r');
plot(time,Output(:,1),'b');
grid on
xlabel('Time (sec)');
ylabel('theta (rad)');
subplot(4,1,2)
hold on
plot(time,Reference(:,2),'--r');
plot(time,Output(:,3),'b');
grid on
xlabel('Time (sec)');
ylabel('x (m)');
subplot(4,1,3)
hold on
plot(time,Output(:,2),'b');
grid on
xlabel('Time (sec)');
ylabel('theta rate(rad/s)');
subplot(4,1,4)
hold on
plot(time,Output(:,4),'b');
grid on
xlabel('Time (sec)');
ylabel('v(m/s)');
pendulum.m
function dx=pendulum(t,x,flag,control_input)
global A B C D;
u=control_input;
dx=zeros(4,1);
%State equation for one link inverted pendulum
dx=A*x+B*u;
end
Kết quả

PID Invert Pendulum